Skip to content

Changes

Page history
CLean up, figure text etc. authored by René Nilsson's avatar René Nilsson
Show whitespace changes
Inline Side-by-side
Lesson-8-Journal-2.markdown
View page @ b44d2f20
......@@ -44,7 +44,7 @@ Two light sensors are placed in the front of the LEGO car pointing downwards. Ag
The line following capabilities is somewhat improved by adding an extra sensor. The LEGO car now follows the center of the black line instead of an edge. However, the PID regulation is slow. When the LEGO car approaches the black line from an angle the PID regulation is not able to correct for this angle and steer the LEGO car onto the black line. In this case the LEGO car just crosses the line. By inspection the cause of this problem is narrowed down to the motor control which seems relatively slow thereby affecting the PID regulation.
In the beginning of the lesson it was estimated that the LeJOS `DifferentialPilot` would be the optimal solution for motor control due to its use of the tachometer. Since the turning methods of this class takes a value in degrees and a radius as input it seemed as the obvious choice in order to simply the programming of the turns. When using this class, a speed and an acceleration is defined and in order to steer the `steer()` method is called. This method takes an input from -200 to 200 as input and steers the LEGO car accordingly. The problem is that even at an extreme turn rate (200 or -200) the reaction of the `DifferentialPilot` is too slow, and not extreme enough to keep the robot on track. Therefore sharp turns are excluded when using the differential pilot.
In the beginning of the lesson it was estimated that the LeJOS `DifferentialPilot` would be the optimal solution for motor control due to its use of the tachometer. Since the turning methods of this class takes a value in degrees and a radius as input it seemed as the obvious choice in order to simply the programming of the turns. When using this class, a speed and an acceleration is defined and in order to steer the `steer()` method is called. This method takes an input from -200 to 200 as input and steers the LEGO car accordingly. The problem is that even at an extreme turn rate (200 or -200) the reaction of the `DifferentialPilot` is too slow to keep the robot on track. Therefore sharp turns are excluded when using the differential pilot.
The solution is to change from the `DifferentialPilot` to direct motor control using the leJOS `MotorPort` class. This greatly improves the PID regulation of the LEGO car.
......@@ -53,7 +53,7 @@ The solution is to change from the `DifferentialPilot` to direct motor control u
### Setup
With the plateau detection and line following functionality in place it is time combine these elements into a single program. For this we will use the behavior control paradigm from lesson 7 [4]. The implementation we used in our project follows a slightly different approach. Instead of each behavior containing a `SharedCar` object, each behavior now implements the interface `Behavior`:
With the plateau detection and line following functionality in place it is time to combine these elements into a single program. For this we will use the behavior control paradigm from lesson 7 [4]. The implementation we used in our project follows a slightly different approach. Instead of each behavior containing a `SharedCar` object, each behavior now implements the interface `Behavior`:
```java
public interface Behavior {
......@@ -114,53 +114,11 @@ switch (nextAction) {
```
The FSM is responsible for performing all turns on the track using an instance of the `Car` class provided by the Arbiter. The methods of the `Car` class is described below. By letting the FSM control the stopping mechanism we avoid having a third behavior that uses the light sensor or an additional color sensor to detect when the LEGO car is in the green end zone.
The PlateauPilot performs an action every time a plateau is reached. This is sensed using the gyroscope. In the code snippet below the run function of the PlateauPilot is shown. This function sets the boolean `isPlatueaReached`, which triggers the Arbiter to perform the next action, as described by the state machine above.
```java
public void run() {
while(true)
{
int gyroVal = gyro.readValue();
double filteredVal = oldFilteredVal*alpha + gyroVal*(1-alpha);
oldFilteredVal = filteredVal;
switch (state) {
case idle: //starting in idle
if (filteredVal > gyroOffset + 40 && isAscending)
{
if(System.currentTimeMillis() > timePlateauReached + 2000) {
state = State.plateauReached;
isPlateauReached = true;
}
}
else if (gyroVal < gyroOffset - 40 && !isAscending)
{
if(System.currentTimeMillis() > timePlateauReached + 2000) {
state = State.plateauReached;
isPlateauReached = true;
}
}
break;
case plateauReached:
if (!isPlateauReached) {
state = State.idle;
timePlateauReached = System.currentTimeMillis();
}
break;
default:
break;
}
}
}
```
The gyro values are filtered with an exponential filter to remove unwanted spikes. If the filtered value is 40 degress/second above or below the offset, a plateau is either entered or left. In order not to trigger the next action when leaving a plateau a timing threshold is inserted. This ensures that at least two seconds passes between actions.
### Results
With the current setup the car is able to follow the black line on the first inclined path. However a problem arises in the plateau detection which is illustrated in the following figure.
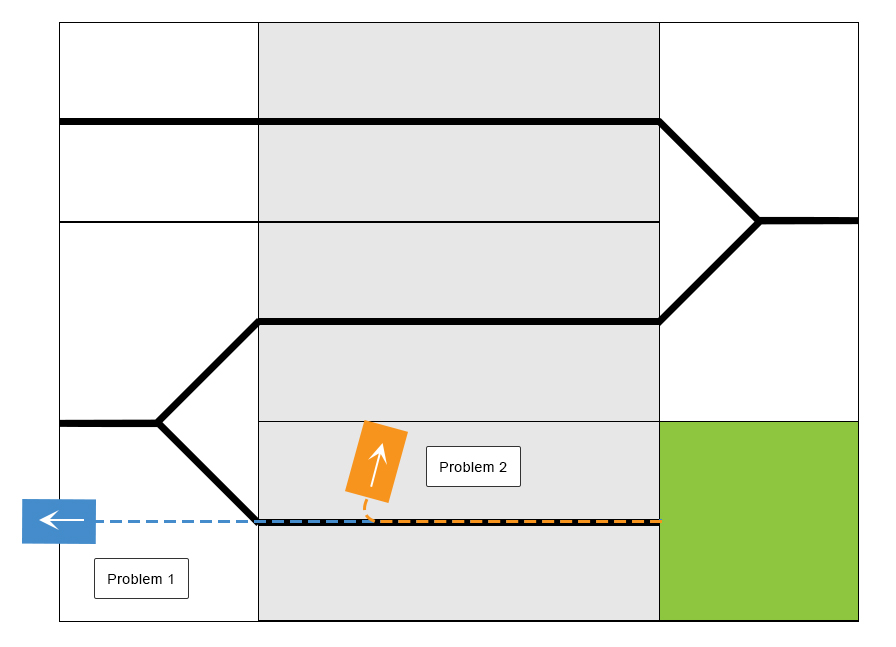
![Problem with correct plateau detection](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/LowGyroProblem.jpg)
![Problem with correct plateau detection.](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/LowGyroProblem.jpg)
A gyroscope threshold determines whether the PlateauPilot behavior is activated. With the threshold too high the plateau is detected to late (Problem 1) and the LEGO car continues out of the track. With the threshold too low the plateau is detected too early and the LEGO car makes a right turn too soon (Problem 2). It seems to be an impossible task to determine this threshold in the current setting.
This indicates that the problem is related to the gyroscope which might not receive enough impact of the incline change when mounted close to the LEGO car in order to determine a sufficient threshold.
......@@ -172,13 +130,13 @@ In this setup the gyroscope is placed relatively low and close to the body of th
The gyroscope is raised by placing it on a long brick as shown in the following image.
![Lego car with the gyro sensor placed higher](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/HighGyroscope.JPG)
![High and low gyroscope mounts.](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/HighGyroscope.JPG)
### Results
The program used to test the gyroscope earlier (Described in section "Gyro measurements on a plateau") is used again with the new setup. The result is seen in the following image where the high mounted gyroscope data is plotted together with the low mounted gyroscope data.
![High gyroscope test](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/GyroHighLowMount.png)
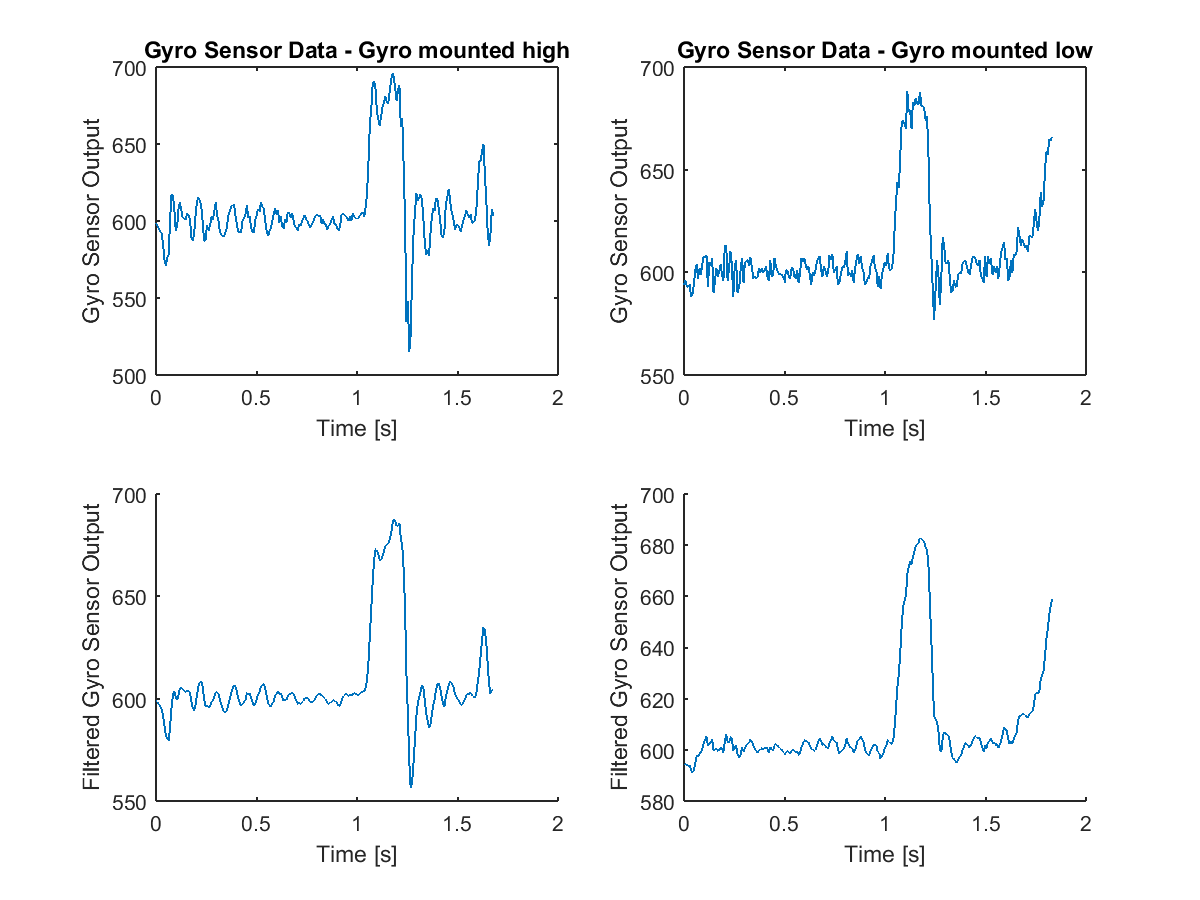
![Gyroscope mounting test: The figure shows both raw and filtered gyroscope output for a high and a low mounted gyroscope. Both tests shows the gyroscope output when the lego car entered the first plateau on the Alishan track, from below.](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/GyroHighLowMount.png)
Although the high mounted gyroscope has a minor negative peak compared to the mean value the two settings (high and low mounted gyroscope) are almost identical and the problem must therefore be located elsewhere.
......@@ -208,9 +166,9 @@ The `gyroOffset` is set to `600` according to the noise floor of the gyroscope t
By implementing these modification to the software and tuning the PID parameters and the hard coded turns, the LEGO car is able to drive all the way to the top of the track. On the top plateau the LEGO car performs a 180 degree turn and initiates its way back. Here a new problem arises. Whenever the LEGO car gets off the top plateau it almost immediately makes a left turn as illustrated in the following figure.
![Problems on the way back](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/DirectMotorControlProblem.jpg)
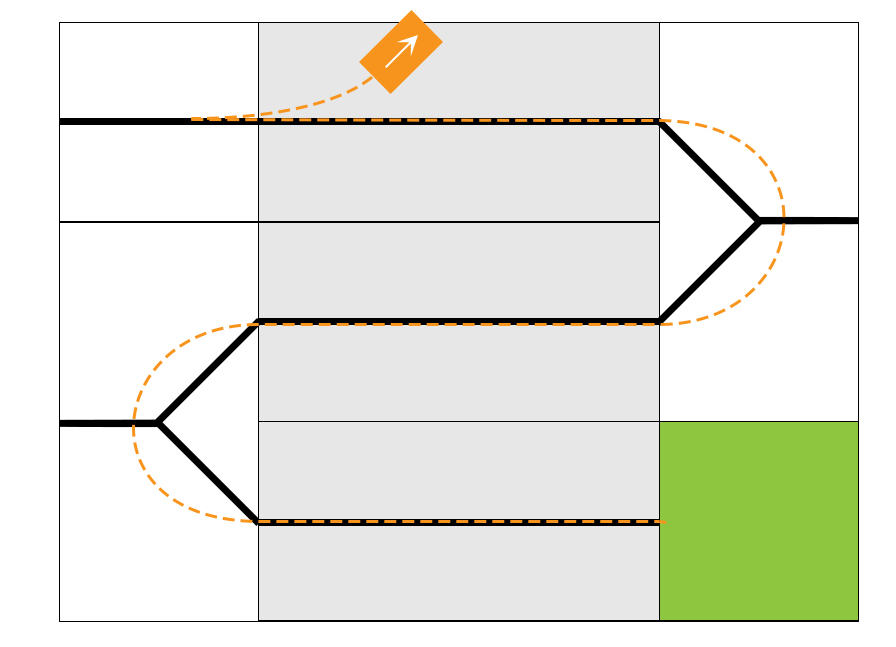
![Illustration of the car track, with problems when descending.](https://gitlab.au.dk/rene2014/lego/raw/master/Lesson8/Images/DirectMotorControlProblem.jpg)
It is assumed that the cause of this is found in the direct motor control implementation. Without any motor regulation the LEGO car quickly gains too much speed when driving down wards the track and the PID regulator cannot cope with this.
It is assumed that the cause of this is found in the direct motor control implementation. Without any motor regulation the LEGO car quickly gains too much speed when driving down the track and the PID regulator cannot cope with this.
The differential pilot seemed to be too high an abstraction level and the direct motor control was too low. Therefore a middle ground is chosen for the motor control which is the NXTRegulatedMotor class.
......@@ -238,7 +196,7 @@ public void Rotate180()
}
```
When turning on each plateau, the robot must travel along an arc of instead of turning around its center. This is not easily implemented using the `rotate()` function, instead each turn is hard coded by imposing a certain power to each motor in a fixed amount of time. The amount of power and the time interval is then adjusted according to manual inspection. Turning is different whether the robot is ascending or descending, and left and right turns are not implemented precisely symmetrical, because the left and right motors run slightly different. All turns follow the same pattern and is implemented as follows:
When turning on each plateau, the robot must travel along an arc instead of turning around its center. This is not easily implemented using the `rotate()` function, instead each turn is hard coded by imposing a certain speed to each motor in a fixed amount of time. The speed and the time interval is then adjusted according to manual inspection. Turning is different whether the robot is ascending or descending, and left and right turns are not implemented precisely symmetrical, because the left and right motors run slightly different. All turns follow the same pattern and is implemented as follows:
```java
public void TurnRightUp()
......@@ -252,7 +210,7 @@ public void TurnRightUp()
}
```
A link to the final code, [RoboRacerV3], is also found in the references section. The references
A link to the final code, [RoboRacerV3], is also found in the references section.
## Conclusion
......